Category Archives: Classwork

Arrays: Preparing for assessments

Preparing for assessments

Your notes should include:

All loops syntax: while, do while, and for.
The Scanner class: how to create an object of it and use it’s methods.
The Math.random() function.
Typical array-processing code highlights:
- 1D and 2D arrays: how to declare and initialize them.
- Code snippets to print all the elements, to add columns, rows.
- Programs designed to create frequency arrays.
- The code needed to swap elements of an array, to find the max and the min.
- A short program to simulate rolling dice.
StdIn, StdOut and StdDraw short API’s with few examples.
The rules to print formatted output, printf.
Simple drawings programs.

Arrays: Test Review Arrays

Arrays Test Review

One Dimensional arrays:
1. Create arrays and initialize them with a loop.
2. Initialize an array when created.
3. Find the number of elements in an array.
4. Check an array’s bounds.
5. Swapping elements of an array – permutations (sampling without replacement)
6. Given an array of N elements, write the code to shuffle them using the random feature.
7. Find the max – min of the elements.
8. Reverse the elements.
9. Find the average of the elements.
10. Print each element.
11. Sieve of Erasthostenes http://en.wikipedia.org/wiki/Sieve_of_Eratosthenes
12. Arrays as frequency or counters.
13. What types must be used as indices for arrays?

Midterm Review Part 1

Content for some questions:

Overflow

From

The int data type is a 32-bit signed two’s complement integer. It has a minimum value of -2,147,483,648 (0x80000000) and a maximum value of 2,147,483,647 (0x7FFFFFFF) (inclusive)

So when you add one to an integer’s max value:

0x7FFFFFFF + 0x00000001 = 0x80000000 (-2,147,483,648)

Arrays: Intro

Typical array-processing code.
Programming with arrays.
- Zero-based indexing
- Array length
- Memory representation
- Bounds checking
- Setting array values at compile time
- Setting array values at run time
Shuffling and sampling
- Exchange
- Shuffling
- Hardwired constants
- Sampling without replacement

classwork:
Write a program, ArrayBasics_YI.java to do the following:

Create an array a[] size 10. Assign a random number between 1 and 30 to each element.
a. Display the first element of the array.
b. Display the last element of the array assuming you do not know the size of the array.
c. Display the messages given when you try to access an element with a negative index and with an index beyond the size of the array.
Create two arrays, suit[] and face_value[].
a. The suit[] array contains the 4 different suits as elements.
b. The face_value array contains “2”, “3”,…,”Jack”,…,”Ace” elements.
c. Use the random function to select five cards and display them.
Create two arrays x[] and y[] with N number of elements both. Prompt the user for N. Assign random integers to each element. Then have another loop to find the product of each element wit the same index and add them all together. This operation is called the “dot product”.

Assignments:
ClosestPair_YI.java
Write a program to create an array of 100 random integers between the values of 1 and 1000 and find the two consecutive integers with the smallest difference between the two of them.

MaxInArray_YI.java
Write a program to create an array of 100 random integers between the values of 1 and 1000 and find the largest value.

AverageArray_YI.java
Write a program to create an array of 100 random integers between the values of 1 and 1000 and find the average of all the elements of the array.

PrintArray_YI.java
Write a program to create an array of 100 random integers between the values of 1 and 1000 and print them separated by 3 spaces. Note: Use printf to keep all your numbers tab properly.
A printf format reference page (cheat sheet)

Pop Quiz Array 1
Pop Quiz 1: Fix the problem

Arrays: Duplicate

Classwork/Homework:
Write a program, Duplicate_YI.java to find a duplicate. Given an array of N elements with each element between 1 and N, write an algorithm to determine whether there are any duplicates. You do not need to preserve the contents of the given array, but do not use an extra array.

Create an array with 50 random integer numbers between 1 and 50 inclusive.
Print the array in 10 rows by 5 columns. Use “printf” to keep the columns aligned.
Print all the duplicate values and their index. Format: value, index 1, index 2 … per line.
Print the total number of duplicates as the last message in your output.

Arrays: At Least One of Each

Classwork/Homework:
Suppose that you have a shuffled deck of cards and you turn them face up, one by one. How many cards do you need to turn up before you have seen one of each suit?
OneOfEach1_YI.java: this program will allow the user to pick as many cards as needed until all the different values in any deck of cards come up. Your program should generate the number of cards needed to find all the suits. The input should be M, the number of suits.

In general, suppose that a trading card company issues trading cards with M different possible cards: how many do you have to collect before you have all M possibilities, assuming that each possibility is equally likely for each card that you collect and that there is an infinite number of cards?

A good example would be “Collect all ranks in a random sequence of cards (M = 13).” Look at page 23 on the pdf above.

Card collector simulation
• Generate random int values between 0 and M-1

• Count number used to generate each value at least once.

Key to the implementation
• Create a boolean array of length M (Initially all false by default.)
• When r generated, check the rth value in the array.
• If true, ignore it (not new).
• If false, count it as new (and set rth entry to true)

How many cards do you need to turn up before you have seen one of each suit? Sample test runs:

How many different cards in your deck? 13
After randomly drawing 46 cards, the full collection was acquired.

How many different cards in your deck? 13
After randomly drawing 22 cards, the full collection was acquired.

How many different cards in your deck? 13
After randomly drawing 49 cards, the full collection was acquired.

How many different cards in your deck? 13
After randomly drawing 30 cards, the full collection was acquired.

OneOfEach2_YI.java: implement this program to allow the user an additional input, the specific number of trials. Each trial will calculate how many cards (no_of_cards) were drawn until all different (face) value cards were drawn. End the program by displaying the average number of cards needed for all the M cards to come up. Again, assuming there is an infinite number of cards.

A large number of trials will give you a better approximation to the solution to the problem. The idea is to keep track of how many cards were drawn to get all the (face) values at each trial and find the average. The more trials, the closer you get to the actual number. You will also see that as the number of trials keeps on growing the average does not change much. To help you find a pattern, then you increase the number of suits, and repeatedly increase the number of trials.

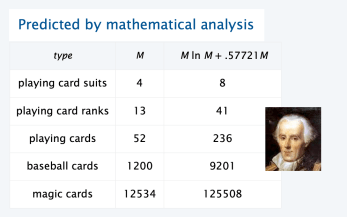
Show these predicted values by running the program with a high number of trials, from 1000 to 1000000.

Sample runs:

% java OneOfEach2_YI 4 1000000
8
% java OneOfEach2_YI 13 1000000
41
% java OneOfEach2_YI 52 100000
236
% java OneOfEach2_YI 1200 10000
9176
% java OneOfEach2_YI 12534 1000
125920

In theory:
Given n different suits, how many cards do you expect you need to draw with replacement (or in this case, an infinite number of cards of all different suits) before having drawn each suit at least once? The mathematical analysis of the problem reveals that the expected number of trials needed approximates n(log(n)).
For example, when n = 50 it takes about 225 trials to collect all 50 suits.

Screen Shot 2015-12-13 at 8.01.43 AM

From Lawerence Chen
Screen Shot 2015-12-13 at 7.56.00 AM

Input/Output: Graphics: Simple Bar Graph

Looking at the printf method
A printf format reference page (cheat sheet)

// This class shows how to initialize an array 
// How to use the printf output formatting method
public class InitPrintfArray 
{
   public static void main( String[] args )
   {
      // initializing the array when it is created
      int[] arrayA = { 87,56,78,99,102 };

      System.out.printf( "%s%7s\n", "Index", "Value" ); // column headings
   
      // output each array element's value 
      for ( int i = 0; i < arrayA.length; i++ )
         System.out.printf( "%5d%5d\n", i, arrayA[ i ] );
   } // end main
} // end class InitPrintfArray

A "simplified" version of a bar chart by using the elements of an array as counters

// Bar graph printing program.

public class BarGraph 
{
   public static void main( String[] args )
   {
      int[] arrayA = { 0, 0, 0, 0, 0, 0, 1, 2, 4, 2, 1 };

      System.out.println( "Grade distribution:" ); 

      // for each array element, output a bar of the chart
      for ( int i = 0; i < arrayA.length; i++ ) 
      {
         // output bar label ( "00-09: ", ..., "90-99: ", "100: " )
         if ( i == 10 )
            System.out.printf( "%5d: ", 100 ); 
         else
            System.out.printf( "%02d-%02d: ", 
               i * 10, i * 10 + 9  ); 
 
         // print bar of asterisks
         for ( int stars = 0; stars < arrayA[ i ]; stars++ )
            System.out.print( "*" );

         System.out.println(); // start a new line of output
      } // end outer for
   } // end main
} // end class BarGraph

Grade distribution:
00-09:
10-19:
20-29:
30-39:
40-49:
50-59:
60-69: *
70-79: **
80-89: ****
90-99: **
100: *
Claswork/Homework:
Tracing 101: Trace the i, arrayA[i], and the output as the inner and outer loops traverse arrayA.

Arrays: The Locker Puzzle

A school has 100 lockers and 100 students. All lockers are closed on the first day of school. As the students enter, the first student, denoted S1, opens every locker. Then the second student, S2, begins with the second locker, denoted L2, and closes every other locker. Student S3 begins with the third locker and changes every third locker (closes it if it was open, and opens it if it was closed). Student S4 begins with locker L4 and changes every fourth locker. Student S5 starts with L5 and changes every fifth locker, and so on until student S100 changes L100.
After all the students have passed through the building and changed the lockers, which lockers are open?

Write a program, WhichLockers_YI.java to find your answer and display all open locker numbers separated by exactly one space.

Hint: Use an array of 100 Boolean elements, each of which indicates whether a locker is open (true) or closed (false). Initially, all lockers are closed.

Arrays: Magic Square

2D Arrays

Classwork/Homework:
Magic squares. A n × n matrix that is filled with the numbers 1,2,3,…,n^2 is a magic square if the sum of the elements in each row, in each column, and in the two diagonals is the same value.
Write a program that reads in 16 values from the keyboard and tests whether they form a magic square when put into a 4 × 4 array. This is only an example of a 4 x 4 square.

Screen Shot 2014-11-23 at 9.53.25 PM

You need to test two features:
1. Does each of the numbers 1, 2, …, 16 occur in the user input?
2. When the numbers are put into a square, are the sums of the rows, columns, and diagonals equal to each other?

Testing and output:
1. Display the given magic square and the value rows, columns and diagonals add up to.
2. Find one more magic square online, display it and show the value all the columns, rows and diagonals are equal to.
3. Display a square that it is not magic but it follows the rules of being filled 1 through n^2.

NOTE: print the input numbers in matrix format, rows by columns.

Strong Recommendation:
Follow the rules by tracing them on paper first. Then, find a pattern!

Arrays: Sieve of Eratosthenes

Classwork/Homework:
Write a program, YI_ErathosPrimes.java to find the all the prime numbers less than or equal to 120 using the Sieve of Eratosthenes algorithm.

Sieve of Eratosthenes

Mrs. Elias's Intro to Computers (Acc)

Class Website at PHS