Classwork/Homework:
Suppose that you have a shuffled deck of cards and you turn them face up, one by one. How many cards do you need to turn up before you have seen one of each suit?
OneOfEach1_YI.java: this program will allow the user to pick as many cards as needed until all the different values in any deck of cards come up. Your program should generate the number of cards needed to find all the suits. The input should be M, the number of suits.
In general, suppose that a trading card company issues trading cards with M different possible cards: how many do you have to collect before you have all M possibilities, assuming that each possibility is equally likely for each card that you collect and that there is an infinite number of cards?
A good example would be “Collect all ranks in a random sequence of cards (M = 13).” Look at page 23 on the pdf above.
Card collector simulation
• Generate random int values between 0 and M-1
• Count number used to generate each value at least once.
Key to the implementation
• Create a boolean array of length M (Initially all false by default.)
• When r generated, check the rth value in the array.
• If true, ignore it (not new).
• If false, count it as new (and set rth entry to true)
How many cards do you need to turn up before you have seen one of each suit? Sample test runs:
How many different cards in your deck? 13
After randomly drawing 46 cards, the full collection was acquired.
How many different cards in your deck? 13
After randomly drawing 22 cards, the full collection was acquired.
How many different cards in your deck? 13
After randomly drawing 49 cards, the full collection was acquired.
How many different cards in your deck? 13
After randomly drawing 30 cards, the full collection was acquired.
OneOfEach2_YI.java: implement this program to allow the user an additional input, the specific number of trials. Each trial will calculate how many cards (no_of_cards) were drawn until all different (face) value cards were drawn. End the program by displaying the average number of cards needed for all the M cards to come up. Again, assuming there is an infinite number of cards.
A large number of trials will give you a better approximation to the solution to the problem. The idea is to keep track of how many cards were drawn to get all the (face) values at each trial and find the average. The more trials, the closer you get to the actual number. You will also see that as the number of trials keeps on growing the average does not change much. To help you find a pattern, then you increase the number of suits, and repeatedly increase the number of trials.
Show these predicted values by running the program with a high number of trials, from 1000 to 1000000.
Sample runs:
% java OneOfEach2_YI 4 1000000
8
% java OneOfEach2_YI 13 1000000
41
% java OneOfEach2_YI 52 100000
236
% java OneOfEach2_YI 1200 10000
9176
% java OneOfEach2_YI 12534 1000
125920
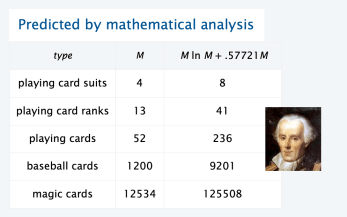
In theory:
Given n different suits, how many cards do you expect you need to draw with replacement (or in this case, an infinite number of cards of all different suits) before having drawn each suit at least once? The mathematical analysis of the problem reveals that the expected number of trials needed approximates n(log(n)).
For example, when n = 50 it takes about 225 trials to collect all 50 suits.

From Lawerence Chen